Penomoran teorema
Sampai di sini, kita telah memiliki delapan teorema, yang dinomori dari T1 hingga T8. Untuk menomori teorema, kita harus berpegang pada aturan ini: Teorema yang dibuktikan oleh teorema yang lain, nomornya harus lebih besar dari teorema yang dipakai untuk membuktikan.
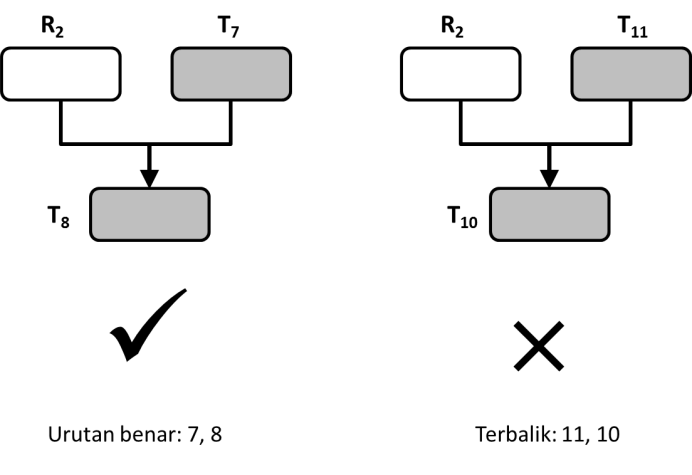
Contohnya adalah teorema 8. T8 dibuktikan menggunakan T7. Berarti penomoran T8 sudah tepat, karena T7 harus dibuktikan sebelum T8, dan T8 menggunakan T7 dalam pembuktiannya (Peringatan: mungkin kamu perlu membaca kalimat ini berulang-ulang untuk memahaminya).
Seandainya saya mengganti nomor T8 dengan T10, dan T7 dengan T11, ini akan menyalahi aturan penomoran, karena ini berarti T11 akan dipakai untuk membuktikan T10.
Ini tidak menjadi masalah jika teorema tidak dibuktikan menggunakan teorema lainnya. Contohnya adalah teorema 5 dan 6. Tidak masalah namanya T5, T6 atau T6, T5, karena yang satu tidak bergantung dari yang lain.

Sistem Penomoran Gödel
Dalam sistem penomoran Gödel, setiap teorema diberi nomor berupa bilangan yang sangat besar. Bilangan besar itu diperoleh dengan cara menerjemahkan masing-masing simbol yang digunakan. Masing-masing simbol memiliki bilangannya sendiri. Misalnya, kita dapat menerjemahkan masing-masing simbol menjadi bilangan menggunakan tabel berikut:
| ∀ | x | ∈ | D | : | A |
|---|---|---|---|---|---|
| 41 | 13 | 51 | 61 | 43 | 91 |
| m | ( | ) | , | ¬ | B |
| 71 | 81 | 82 | 83 | 35 | 92 |
Dengan demikian, sebuah aturan yang berbunyi:
Aturan tersebut dapat diterjemahkan dari kiri ke kanan sesuai tabel, sehingga akan memiliki nomor:
4.113.516.143.718.113.831.382
Di tempat lain, jika ada teorema yang berbunyi:
Teorema tersebut akan diberi nomor:
35.718.191.839.282.
4.113.516.143.718.113.831.382 : ∀x∈D: m(x,x)
35.718.191.839.282 :¬m(A, B)
Dengan sistem ini, sebuah nomor teorema akan mewakili kalimat teorema tersebut. Kita dapat menerjemahkan kembali kalimat teorema dari nomornya menggunakan tabel yang sama.
Sistem penomoran Gödel tidak digunakan untuk pembuktian yang sebenarnya. Sistem ini digunakan oleh Gödel untuk keperluan filosofis: Membuktikan bahwa jika aritmetika konsisten, aritmetika tidak akan pernah komplet. Pembuktian ini adalah salah satu pembuktian terpenting dalam abad 20 yang mempengaruhi filsafat dan ilmu pengetahuan. Kita akan meninjau hal ini lebih dalam pada bab berikutnya.
Walaupun tidak digunakan dalam pembuktian, sistem serupa sebenarnya digunakan dalam komputer yang kamu pakai. Setiap kalimat dalam komputer adalah rangkaian bilangan. Kata TOLONG
misalnya, disimpan dalam memori komputer sebagai bilangan biner 01010100 01001111 01001100 01001111 01001110 01000111, yang dalam bilangan desimal nilainya adalah 92.699.559.415.367.
Berikutnya: Metode pembuktian langsung