Keunikan

Menurutku, kamu orangnya unik.

Apakah artinya unik? Unik berarti tiada duanya. Suatu relasi biner disebut sebagai unik kanan jika setiap panah yang keluar dari masing-masing domain tidak lebih dari satu, ditandai dengan panah yang tidak bercabang.

Sebaliknya, unik kiri jika setiap panah yang sampai pada kodomain adalah masing-masing tidak lebih dari satu.

Unik kanan

Sebutkan sifat yang dimiliki relasi dalam diagram berikut ini.

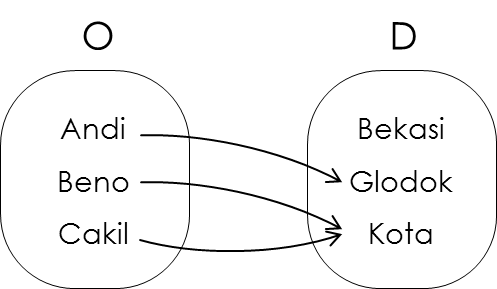
Relasi pada himpunan O dan D pada contoh di atas bersifat unik kanan. Terlihat bahwa untuk masing-masing anggota domain O (Andi, Beno, dan Cakil) terhubung kepada hanya satu anggota D.

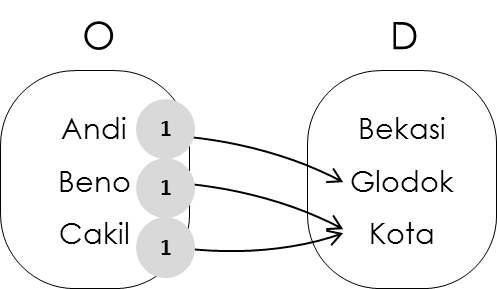
Perhatikan bahwa hal ini dapat dengan mudah disalahpahami. Yang dimaksud pada hanya satu anggota D adalah satu anggota O untuk satu anggota D.

• Andi untuk satu anggota D, yaitu Glodok

• Beno untuk satu anggota D, yaitu Kota

• Cakil untuk satu anggota D, yaitu Kota

Bandingkan dengan yang sebaliknya.

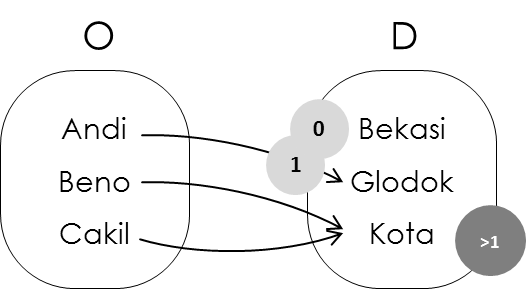
• Bekasi tidak dapat panah.

• Glodok dapat satu panah.

• Kota dapat lebih dari satu panah. Ini melanggar sifat unik kiri.

Ditambah dengan informasi pada contoh-contoh sebelumnya, relasi di atas memiliki sifat:

• Total kiri

• Tidak total kanan

• Unik kanan

• Tidak unik kiri

Perhatikan bahwa berbeda dengan sifat total kiri yang membicarakan himpunan di sebelah kiri, sifat unik kiri justru membicarakan himpunan yang di sebelah kanan.

Unik tidak harus total

Sangat mudah untuk mencampur adukkan antara syarat sifat total dan unik. Relasi di bawah ini:

• Tidak total kiri

• Tidak total kanan

• Unik kanan

• Unik kiri

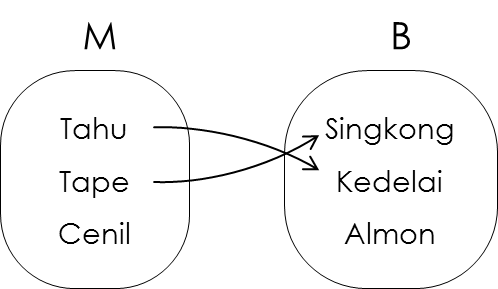
Jelaskan alasannya!

Namun kadang-kadang total

Sebutkan sifat-sifat yang dimiliki relasi berikut ini.

Relasi tersebut memiliki sifat:

• Total kiri, karena setiap anggota H terhubung dengan anggota B.

• Tidak total kanan, karena ada anggota B yang tidak terhubung dengan anggota H (yang mana?).

• Tidak unik kanan, karena ada anggota H yang memiliki panah kanan bercabang (yang mana?).

• Tidak unik kiri.

Jomblo dan selingkuh

Kamu bisa memahami konsep total dan unik dengan konsep ini: Jomblo dan selingkuh. Suatu relasi disebut total jika relasi itu tidak mengandung jomblo, dan disebut unik jika relasi itu tidak mengandung selingkuh.

TOTAL = NO JOMBLO

UNIK = NO SELINGKUH

Contohnya relasi berikut ini bersifat total kanan dan unik kiri tetapi tidak total kiri maupun unik kanan. Di bagian domain ada yang jomblo, berarti tidak total kiri. Ada yang selingkuh juga, berarti tidak unik kanan. Sebaliknya, di bagian kodomain tidak ada yang jomblo berarti total kanan. Juga tidak ada yang selingkuh berarti unik kiri. Alangkah indahnya jika setiap relasi asmara dalam suatu masyarakat bersifat total dan unik.

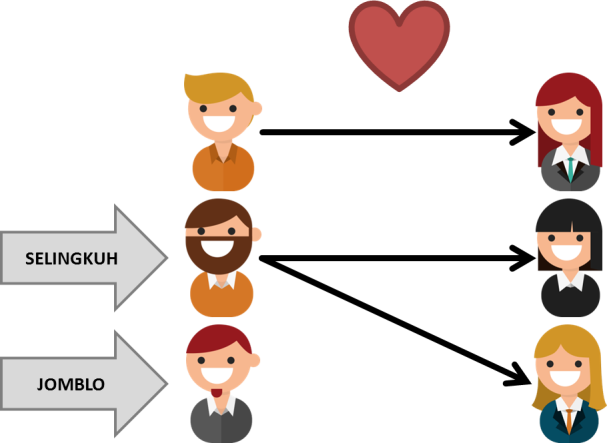
Catatan: Tidak ada maksud tertentu ketika menempatkan contoh yang selingkuh pada pihak laki-laki.

Pertanyaan: Apakah buku matematika yang mengandung kata selingkuh mengajarkan murid untuk selingkuh?

Latihan

1. Lingkari elemen yang menyebabkan tidak unik, dan kotaki elemen yang menyebabkan tidak total.

1. P = {a, b, c, d} dan Q = {0, 5, 9}. Dari setiap himpunan penyelesaian relasi P ke Q berikut, gambarkan diagram kartesiusnya, kemudian tentukan sifat-sifatnya.

   2. {(a, 5), (b, 9), (a, 0), (c, 5)}
   3. {(a, 5), (b, 9), (c, 0), (d, 0)}
   4. {(a, 5), (b, 5), (c, 9), (d, 5)}
   5. {(a, 5), (b, 0), (c, 9)}
   6. {(b, 0), (c, 0), (a, 0), (d, 0)}
   7. {(b, 5), (c, 9), (d, 0)}
   8. {(a, 5), (c, 9), (c, 5), (d, 0)}

2. Bagaimanakah ciri-ciri sifat total dan sifat unik pada diagram kartesius nomor sebelumnya?

Untuk domain kontinu

Diberikan x, y ∈ Himpunan persegi dalam bidang Kartesius yang memiliki sisi yang sejajar dengan sumbu X. Tentukan totalitas dan keunikan relasi, x memiliki sisi yang juga adalah sisi y.

Dalam contoh-contoh sebelumnya, himpunan yang diberikan memiliki sedikit anggota. Namun persegi yang sifatnya seperti yang disebutkan di atas ada banyak sekali. Ada tak berhingga! Gambar di bawah ini hanya memperlihatkan empat di antaranya.

Tidak masalah. Kita tetap dapat menentukan sifat total dan uniknya.

Sifat total kiri berarti untuk setiap persegi x, ada persegi y yang memiliki sisi yang sama dengan x. Contohnya adalah:

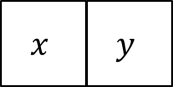
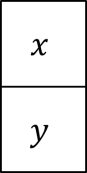
Jangan lupakan juga kasus khusus berikut ini, yaitu x dan y adalah persegi yang sama.

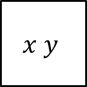
Apakah semua persegi yang sesuai definisi memiliki sifat tersebut? Tentu saja. Kita selalu dapat membuat persegi lain yang memiliki sisi yang sama dengan persegi apapun yang kita miliki.

Setidaknya, persegi itu sendiri juga memiliki sisi yang sama dengan dirinya sendiri. Ini berlaku untuk setiap persegi. Karena itu, relasi ini bersifat total kiri. Dengan cara yang sama, kamu dapat membuktikan bahwa relasi ini total kanan.

Selanjutnya, sifat unik kanan berarti untuk setiap persegi x, hanya boleh ada paling banyak satu persegi y yang mengandung sisi yang sama. Ini jelas tidak mungkin, karena dari gambar di atas, setidaknya ada satu persegi yang bisa memiliki lima persegi y yang berbagi sisi dengannya. Karena itulah relasi ini tidak bersifat unik kanan, yang juga dengan cara yang sama dapat dibuktikan bahwa relasi ini tidak unik kiri.

Latihan

1. Diberikan x, y ∈ Himpunan garis lurus dalam bidang datar. Tentukan totalitas dan keunikan relasi:

   2. x tegak lurus dengan y.
   3. x sejajar dengan y.
   4. x berimpit dengan y.

2. Jika x, y ∈ Himpunan segitiga dalam bidang datar, tentukan totalitas dan keunikan relasi:

   6. x sebangun dengan y.
   7. x kongruen dengan y.
   8. Luas x lebih besar dari luas y.
   9. Luas x sama dengan luas y.
   10. x dan y dapat digabungkan menjadi persegi.

3. Tentukan sifat-sifat ketotalan dan keunikan yang dimiliki relasi-relasi berikut.

   12. Negara dengan ibukota.
   13. Negara dengan kepala negara.
   14. Penemu dengan temuannya.
   15. Komposer dengan karyanya.
   16. Karya komposer dengan komposernya.
   17. Manusia dengan DNA-nya.

Berikutnya: Unik kanan