Paradoks Russell

Russell menemukan paradoks dalam teori himpunan yang disusun oleh Gottlob Frege. Dalam teori himpunan Frege, untuk setiap kalimat terbuka p(x), dapat dibuat himpunan yang mengandung objek-objek yang sesuai dengan yang dideskripsikan oleh p(x). Contoh-contohya adalah sebagai berikut:

x bukan anggota x.

Berarti seharusnya akan ada himpunan yang anggotanya sesuai dengan kalimat tersebut.

Himpunan dari semua himpunan

Himpunan A di atas mewakili konsep, Himpunan dari semua himpunan yang tidak mengandung dirinya sendiri. Konsep ini tidak mungkin mendeskripsikan himpunan apapun, yang berarti bahwa teori Frege salah.

Mungkin kita dapat dengan mudah mengatakan bahwa Bertrand Russell pasti termasuk dalam himpunan A, karena Bertrand Russell bukanlah himpunan, sehingga Bertrand Russell ∉ Bertrand Russell.

Demikian juga dengan objek-objek lain. Bilangan 1 bukanlah anggota dari bilangan 1. Himpunan bilangan asli ℕ juga bukanlah anggota dari himpunan bilangan asli (ℕ ∉ ℕ). Akibatnya, 1 maupun ℕ akan termasuk di dalam A.

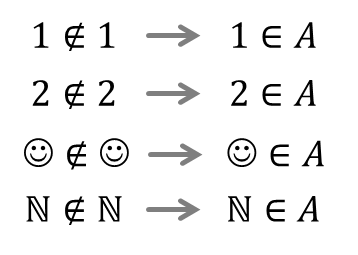
Karena itu himpunan A akan berisi banyak sekali anggota.

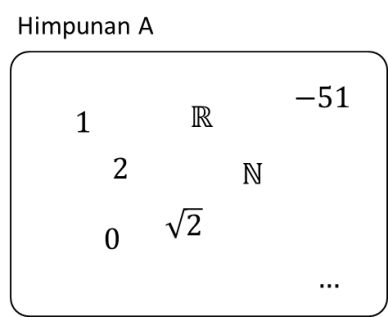
Namun bagaimana dengan himpunan A sendiri? Apakah terdapat di dalam A?

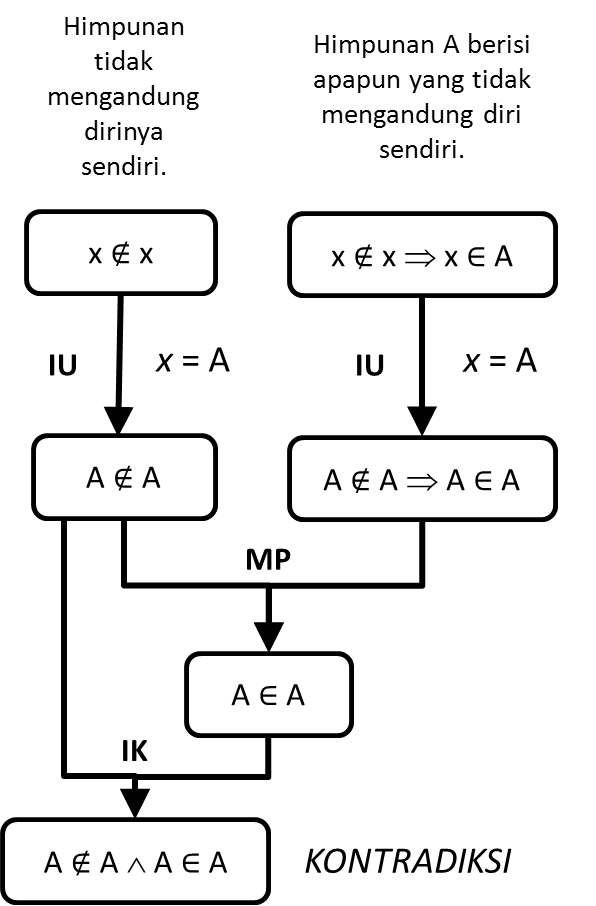
Jika A terdapat di dalam A, ini akan kontradiksi dengan kalimat tersebut, karena x \notin x juga berarti A \notin A. Artinya himpunan A pasti tidak mengandung A.

Sebaliknya, karena A \notin A, menurut deskripsi himpunan A, semua yang bukan anggota dirinya sendiri adalah anggota A. Berarti karena A \notin A, maka A adalah anggota A.

Kamu tidak perlu memikirkan ini terus menerus, karena ini akan berulang terus dan hasilnya sudah jelas: kontradiksi. Artinya ada yang salah dengan aksioma Frege ini. Jadi dua pernyataan ini, yaitu A \in A dan A \notin A sama-sama dihasilkan dalam teori Frege. Ternyata teori Frege mengandung kontradiksi.

Berikutnya: Teori tipe